2023. 4. 4. 00:31ㆍ_Study/Baekjoon
| 백준 문제풀이 | python | ||
| No. 11004 K번째 수 | |||
#파이썬 #백준 #문제풀이 #11004 K번째 수
11004번: K번째 수
수 N개 A1, A2, ..., AN이 주어진다. A를 오름차순 정렬했을 때, 앞에서부터 K번째 있는 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
이번 글에서는 퀵정렬을 구현하는데 중점을 둔다.

예제 입력 1
5 2
4 1 2 3 5예제 출력 1
2
// 알고리즘
가장 중요한 목적이 무엇인지?
파이썬 라이브러리에서 제공해주는 .sort()함수를 사용해서 풀어본다.
퀵정렬을 구현해보고 최악의 경우 O(n^2)의 시간복잡도를 가진다는 것을 확인한다.
그리고 병합정렬도 구현하여 시간복잡도 제한에서 통과한다.
왜 이런 방법을 선택했는지?
sort함수를 사용하면 간단하게 구현할 수 있지만, 퀵정렬과 병합정렬을 공부하기 위해서 직접 구현해보기로 하였다.
// 계획하기
| 함수명 | 설명 | ||
| 1. | quickSort(S,E,K) | 퀵 정렬을 하되, K번째 수를 찾는다. | |
| 2. | partition(S,E) | 피벗 구하기 함수 | |
| 3. | swap(a,b) | a,b를 바꾼다 |
// 구현하기
-> How?
어떻게 구현?
#퀵정렬
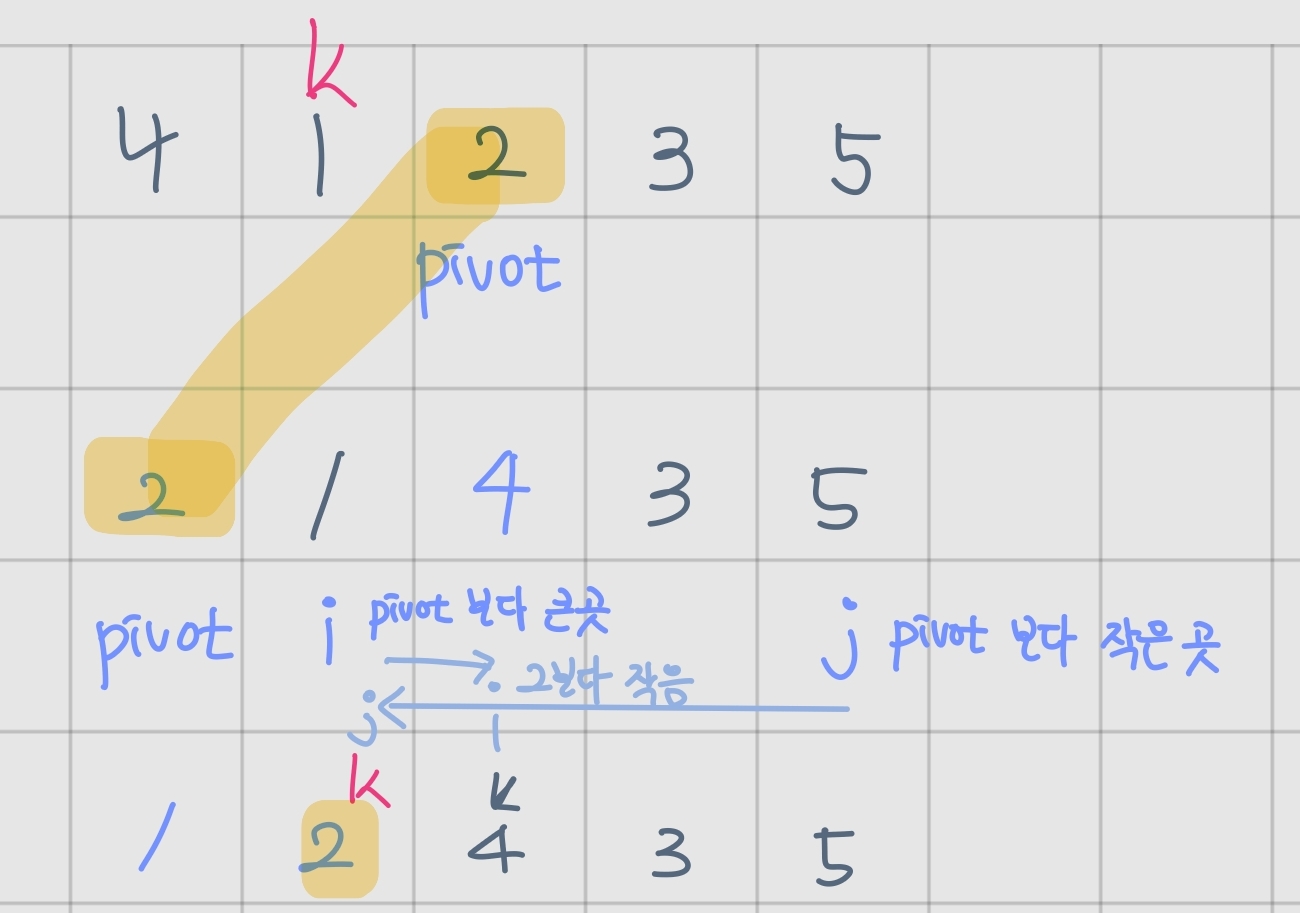
1. pivot 의 이동
퀵정렬은 pivot 값에 따라 시간복잡도가 크게 달라질 수 있다.
먼저 생각해보면, pivot값을 중간으로 하는 경우 배열 양쪽이 쪼개져서 연산하기 힘들기 때문에 pivot을 맨 앞이나 맨 끝으로 이동한다.

2. j와 i의 이동과 반복문의 조건
- j가 pivot보다 크면 j--연산을 반복하며 이동하게 되고 : j는 큰 값이 모이는 곳
- i가 pivot보다 작으면서 j가 계속 큰 경우 i++연산을 반복 : i는 pivot보다 작은 값이 모이는 곳
i와 j 가 만나면 정렬이 끝났으므로 반복문을 빠져나온다.

3. pivot 돌려놓기
두 집합이 pivot을 기준으로 나뉘었기 때문에 이를 swap 한다.
이때 pivot값이 위치하는 곳은 고정된다.

4. K번째수를 구한다.
QuickSort: Cache를 사용하는 함수
def quicksort(x):
if len(x) <= 1:
return x
pivot = x[len(x) // 2]
less = []
more = []
equal = []
for a in x:
if a < pivot:
less.append(a)
elif a > pivot:
more.append(a)
else:
equal.append(a)
return quicksort(less) + equal + quicksort(more)
단순 퀵정렬 사용시 시간 초과가 된다. 연산횟수를 크게 줄여야한다.
N, K = (map(int,input().split()))
lists = list(map(int,input().split()))
def solution(N,K,lists):
answer = 0
quicksort(lists)
answer = lists[K]
return answer
def quicksort(x):
if len(x) <= 1:
return x
pivot = x[len(x) // 2]
less = []
more = []
equal = []
for a in x:
if a < pivot:
less.append(a)
elif a > pivot:
more.append(a)
else:
equal.append(a)
return quicksort(less) + equal + quicksort(more)
print(solution(N,K,lists))
// cache 없는 슈도코드
N K = input
arr = input
#퀵정렬함수 (처음, 끝, K):
if (처음 < 끝): #정렬이 계속되는 경우에
pivot = 피벗 구하기 함수(i,j,K):
# K를 찾으므로 pivot을 기준으로 앞쪽 정렬이 끝났으면 끝낸다.
if(K < pivot):
왼쪽 퀵정렬함수(i,pivot-1,K)
elif ( K > pivot):
오른쪽 퀵정렬함수 (pivot,j,K)
else : (pivot == K)
return
# 피벗 구하기함수(S,E,K):
#데이터가 2개인 경우 바로 정렬
if(S +1 == E): 인 경우
if ( 왼쪽이 더 크다면)
swap(i,j)
return E
pivot = i+j // 2
swap(S, pivot) # 연산하기 쉽게 맨 앞으로 미리 보내기
i = S+1 #양옆 선택하기
j = E
while(i<j):
if(arr[pivot] > arr[i] and i가 len(arr)-1 보다 작아야 index오류 발생 x) #작은경우 그리고
i++
if(arr[pivot] < arr[j] and j>0) # 큰경우 j가 0으로 가면 안됨 pivot의 영역
j--
if (i <= j)
swap(i,j) # 이미 정렬?
i++ j--
#다시 pivot을 중앙값으로 원래대로 돌려놓기
S랑 pivot 교환
그리고 j가 pivot의 자리라서
return j
swap 이 상당히 많다. swap 함수를 차라리 만드는 것이 낫다.
# swap(a,b)
global lists
lists[a], lists[b] = lists[b], lists[a]
global 변수를 잊지말기
// 손코딩
def quicksort(S,E,K):
global lists
if (S < E):
pivot = partition(S,E)
if (pivot < K):
quicksort(pivot+1,E,K)
elif (K < E):
quicksort(S,pivot-1,K)
else:
return
->Why?
왜 이런 방법을?
// 수정하기
index오류나 퀵정렬의 결과값이 살짝 달라서 손코딩으로 디버깅하였다.
while ( arr[pivot] > arr[i] and i < len(arr)-1 ): 에서 i > len(arr)-1로 잘못 코딩하여 다른 값을 swap하고 있었다.
QuickSort pypy3로 제출시 통과된다.
python3도 제출시 통과된다.

// 완성코드 sort를 사용한 방법
import math
N, K = (map(int,input().split()))
lists = list(map(int,input().split()))
def solution(N,K,lists):
answer = 0
lists.sort()
answer = lists[K-1]
return answer
print(solution(N,K,lists))
// 완성코드 Quicksort를 사용한 방법
N, K = (map(int,input().split()))
lists = list(map(int,input().split()))
def solution(N,K,lists):
answer = 0
quicksort(0,N-1,K-1)
answer = lists[K-1]
return answer
def quicksort(S,E,K):
global lists
if (S < E):
pivot = partition(S,E)
if (pivot < K):
quicksort(pivot+1,E,K)
elif (K < pivot):
quicksort(S,pivot-1,K)
else:
return
def partition(S,E):
global lists
#데이터가 2개인 경우 바로 비교해서 정렬
if(S+1 == E):
if lists[S] > lists[E]:
swap(S,E)
return E
pivot = (S+E)//2
swap(S,pivot)
pivot = S
i = S + 1
j = E
while(i<=j):
#피벗보다 큰 수가 나올 때 까지 i 증가
while lists[pivot]> lists[i] and i<len(lists)-1:
i+=1
#피벗보다 작은 수가 나올때 까지 j 감소
while(lists[pivot] < lists[j] and j>0):
j-=1
if i <= j:
swap(i, j)
i += 1
j -= 1
temp = lists[pivot]
lists[S] = lists[j]
lists[j] = temp
return j
def swap(a,b):
global lists
lists[a], lists[b] = lists[b], lists[a]
print(solution(N,K,lists))
Reference : Do it! 코딩테스트 - 기초편

'_Study > Baekjoon' 카테고리의 다른 글
| [10986] 나머지 합 구하기 #python #백준 (0) | 2023.04.30 |
|---|---|
| [11659] 백준 구간 합 구하기 1 python (0) | 2023.04.25 |
| 프로그래머스 숨어있는 숫자의 덧셈 (2) 파이썬 테스트 2,3,4,5,6,7 실패 해결 (0) | 2023.04.03 |
| 백준, 프로그래머스 자동 커밋, 자동 올리기, 동기화 잔디채우기, 빨간 체크 (2) | 2023.03.15 |
| 프로그래머스 파이썬 문자 반복 출력하기 (0) | 2023.02.24 |